My digits 10 and 11
Throughout all of my conlanging and occasionally my maths writing, it is sometimes needed to add extra glyphs to represent digits in bases greater than 10.
When limited to typing on a computer, I use the general convention of using the letters A to Z to represent the digits from 10 onwards, and then resorting to representing each digit as a base-10 number separated by semicolons if we're going beyond base 36 or if for whatever reason the digits are not sufficiently enlightening. That works well enough for most reasons, and (especially with very high bases) I use it everywhere.
However, when I was young, I found using letters for digits to be unsatisfying, reasoning that they're already being used for variables and so there's a bit of redundancy. Computers weren't widespread at the time and in any case I had no reason to type things as often as I do now, so I went and invented a couple of extra glyphs predicated on composing the established digits from 0 to 9 to form the new digits. And to this day the lower-numbered ones are still in use.
This entry is meant to document these digits so I can point to it later. It might be mirrored to more visible places in the near future.
(It's a bit funny that literally the first entry after the introduction page with the general format breaks that format.)
The digits
So what do they look like? Well, like this:
Digits 10 (left) and 11 (right), in handwritten form
🖼️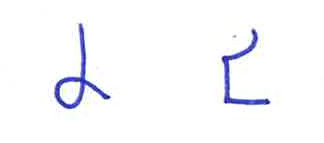
In pixel art form (small, 3 × 5)
🖼️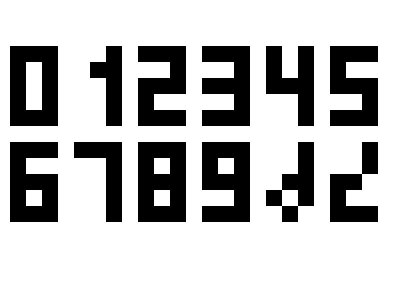
In pixel art form (large, 5 × 7)
🖼️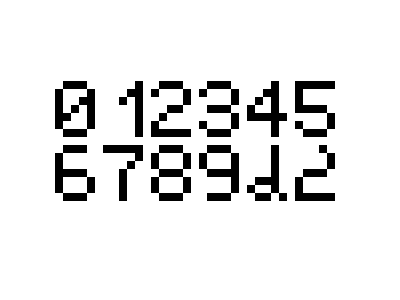
There's no typeset form because I don't know how to make fonts and can't be bothered to learn them. Plus, typesetting them seems largely pointless as there would be no font support for them, though this might change as I write my Drsk grammar.
Graphic etymology
While the digits look fairly arbitrary they aren't. In fact they trace themselves quite nicely through the natural evolution of symbols as they get worn down by ordinary hands.
The digit 10 is created by composing 9 and 1 together.
Here's how it becomes the modern glyph.
🖼️
And similarly, 11 is created by fusing 9 and 2.
🖼️
Each of these are actually used in fact until I wore them down with my own hand.
On beyond 12
Being the enterprising 12-year-old I was, I also built a number of glyphs beyond 19 (my original stopping point). I have long since forgotten most of them, but here's my recreation of the glyphs today up to 35, at which point I would not have used this system. The digits start at 10, go from left to right then top to bottom.
🖼️
The principle of composing to form the new digits remain, but now multiplication is brought into the mix as having to write 9 + 9 + 9 + ⋯ doesn't make for easy glyph making. None of the glyphs past a certain point are actually very satisfying. I never used the larger ones, and only drew them to try and extend the system.
Summary and the future
Although 10 and 11 are heavily used today, and they have been sufficiently worn down to demonstrate it, the rest are less useful and I have never used them much past the original purpose of writing a multiplication table using them. Still, I am very proud of them and use the ones that I do use wherever I can.
I might make a metafont package for 10 and 11. Chuck that into the long to-do list I already have.